| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- graph
- GDB
- GraphX
- 그래프 질의언어
- r
- TensorFlow
- spark
- 딥러닝
- Graph Tech
- Neo4j
- 인공지능
- 빅데이터
- SparkML
- RDD
- 그래프 데이터베이스
- 분산 병렬 처리
- SQL
- TigerGraph
- 연합학습
- Graph Ecosystem
- 그래프 에코시스템
- Python
- graph database
- Federated Learning
- BigData
- Cypher
- 그래프
- GSQL
- RStudio
- DeepLearning
- Today
- Total
Hee'World
가설과 검정 본문
통계적 가설은 통계학에서 사용하는 용어로, 하나의 특정 주장을 모수를 이용해 나타낸 형태를 지칭한다. 가령, '미국 성인여자의 신장은 크다'는 통계적 가설이 될 수 없다. 하지만 '미국 성인여자의 평균신장은 180cm이다.'는 통계적 가설이 될 수 있다. 평균신장은 여기서 모집단 특성을 나타내는 모수의 역할을 수행한다. 통계적 가설은 귀무가설과 이와 반대에 있는 대립가설로 나타낸다.[2]
절차[편집]
가설검정은 다음과 같은 총 5단계 절차를 거치게 된다.[3]
귀무가설과 대립가설 설정[편집]
먼저 연구가설 내용을 통계적 가설로 바꾸어 줌으로써 가설 검정이 시작된다.[2] 통계적 가설은 귀무가설( )과 대립가설(
)과 대립가설( )로 나뉜다.
)로 나뉜다.
가령, 미국 성인여성의 평균신장이 180cm라는 하나의 가설을 검정할 계획이라면, 귀무가설의 표기은 다음과 같다.
 :
: 
해당 귀무가설과 반대되는 대립가설은 다음과 같은 형태가 있다.
- 제1형 :
 :
: 
- 제2형 :
 :
: 
- 제3형 :
 :
: 
여기서 제 1형은 양측검정(two-sided test), 제 2형, 제 3형은 단측검정(one-sided test)이라고 지칭한다. 단측검정을 굳이 나누자면 제 2형은 우측검정이라고 하며, 제 3형을 좌측검정이라고 부른다.
양측검정은 가설검증에서 기각영역이 양쪽에 있는 것이고, 그러므로 유의수준  도 양극단으로 갈라져 한쪽의 면적이
도 양극단으로 갈라져 한쪽의 면적이  가 된다. 기각영역이 어느 한쪽에만 있게 되는 경우를 단측검정이라고 한다. [4]
가 된다. 기각영역이 어느 한쪽에만 있게 되는 경우를 단측검정이라고 한다. [4]
'-http://ko.wikipedia.org/wiki/가설 검정
귀무가설
귀무가설(歸無假說, 영어: null hypothesis, 기호 H0) 또는 영가설(零假說)은 통계학에서 처음부터 버릴 것을 예상하는 가설이다. 차이가 없거나 의미있는 차이가 없는 경우의 가설이며 이것이 맞거나 맞지 않다는 통계학적 증거를 통해 증명하려는 가설이다. 예를 들어 범죄 사건에서 용의자가 있을 때 형사는 이 용의자가 범죄를 저질렀다는 추정인 대립가설을 세우게 된다. 이때 귀무가설은 용의자는 무죄라는 가설이다. 통계적인 방법으로 가설검정을 시도할 때 쓰인다. 로널드 피셔가 1966년에 정의하였다.
예[편집]
기본적으로는 참으로 추정되며 이를 거부하기 위해서는 증거가 꼭 필요하다. 예를 들어 남학생과 여학생들의 두 성적 샘플을 비교해 볼 때, 귀무가설은 남학생들의 평균이 여학생들의 평균과 같은 것이라는 것이다.
- H0 : μ1 = μ2
여기서:
- H0 = 귀무가설
- μ1 = 집단1의 평균
- μ2 = 집단2의 평균
또한 귀무가설이 같은 집단으로부터 뽑힌 두 샘플들이라고 가정하고 그래서 평균과 더불어 분산과 분포는 같다고 가정한다. 이러한 귀무가설의 설정은 통계적 유의성을 시험하는 데 중요한 단계이다. 이러한 가설을 형성하고 얻어진 데이터에서 확률적 검정을 해봄으로써 귀무가설이 예측하는 것이 맞는지 아닌지를 알아 볼 수 있다. 또한 만약 이것이 참이라면 여기서 얻어진 확률은 결과의 유의수준으로 부른다.
- http://ko.wikipedia.org/wiki/%EA%B7%80%EB%AC%B4%EA%B0%80%EC%84%A4
대립가설
가설 검정 이론에서, 대립가설(對立假說, 영어: alternative hypothesis) 또는 연구가설 또는 유지가설은 귀무가설에 대립하는 명제이다. 보통, 모집단에서 독립변수와 결과변수 사이에 어떤 특정한 관련이 있다는 꼴이다. 어떤 가능성에 대해 확률적인 가설검정을 할 때 귀무가설과 함께 사용된다. 이 가설은 귀무가설처럼 검정을 직접 수행하기는 불가능하며 귀무가설을 기각함으로써 받아들여지는 반증의 과정을 거쳐 받아들여질 수 있다.
단측과 양측검정[편집]
대립가설은 양측대립가설과 단측대립가설이 있다.
단측대립가설[편집]
독립변수와 결과변수와의 관련성을 검정할 때 그 방향이 미리 어느 한쪽으로 결정되어 있는 경우이다. 예를 들어 새로 개발된 심장병 치료 약물이 기존의 약물요법에 비교하여 더 효과가 좋은가?라는 것을 밝혀낼 때에 더 효과가 좋다는 가설이 단측대립가설이다.
양측대립가설[편집]
독립변수와 종속변수간에 관련성 혹은 차이가 존재하는가?라는 면에서만 관심을 가지는 것이며 그 방향은 따지지 않는 가설이다. 예를 들어 새로 개발된 심장병 치료 약물이 기존의 약물요법에 비교하여 효과에 차이가 있다라고 가정하는 것이다.
- http://ko.wikipedia.org/wiki/%EB%8C%80%EB%A6%BD%EA%B0%80%EC%84%A4
검정통계량
- http://math7.tistory.com/84
유의수준
유의수준(significance level)은 통계적인 가설검정에서 사용되는 기준값이다. 일반적으로 유의수준은  로 표시하고 95%의 신뢰도를 기준으로 한다면 (1−0.95)인 0.05값이 유의수준 값이 된다. 가설검정의 절차에서 유의수준 값과 유의확률 값을 비교하여 통계적 유의성을 검정하게 된다.
로 표시하고 95%의 신뢰도를 기준으로 한다면 (1−0.95)인 0.05값이 유의수준 값이 된다. 가설검정의 절차에서 유의수준 값과 유의확률 값을 비교하여 통계적 유의성을 검정하게 된다.
http://ko.wikipedia.org/wiki/%EC%9C%A0%EC%9D%98_%EC%88%98%EC%A4%80
유의확률
통계적 가설 검정에서 유의 확률(有意確率, 영어: significance probability) 또는 p값(영어: p-value)은 귀무가설이 맞다고 가정할 때 얻은 결과보다 극단적인 결과가 실제로 관측될 확률이다. 실험의 유의확률은 실험의 표본 공간에서 정의되는 확률변수로서, 0~1 사이의 값을 가진다.
정의[편집]
주어진 표본의 유의 확률은 귀무가설을 가정하였을 때 표본 이상으로 극단적인 결과를 얻을 확률이다. 여기서 "더 극단적"이라는 것은 정의에 따라 다르다. 예를 들어, 정규분포의 경우, 귀무가설을 가정한 실수 확률변수  와 표본
와 표본 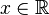 에 대하여 왼쪽 꼬리 유의 확률(영어: left-tail p-value)
에 대하여 왼쪽 꼬리 유의 확률(영어: left-tail p-value)
및 오른쪽 꼬리 유의 확률(영어: right-tail p-value)
및 양쪽 꼬리 유의 확률(영어: double-tail p-value)
를 정의할 수 있다.
만약 확률 변수가 단순한 실수가 아니라면, 더 복잡한 "극단성"을 정의하여야 한다. 예를 들어, 표본이 노름공간에 있는 경우, 노름함수  를 사용하여 표본
를 사용하여 표본  의 유의 확률을
의 유의 확률을
로 정의할 수 있다.
http://ko.wikipedia.org/wiki/%EC%9C%A0%EC%9D%98_%ED%99%95%EB%A5%A0
'Programming > R' 카테고리의 다른 글
| 데이터다루기 (0) | 2015.05.02 |
|---|---|
| [R 머신러닝] 데이터에 맞는 알고리즘 (0) | 2015.05.02 |
| R의 기술통계 명령어 (0) | 2015.03.28 |
| R과 MySQL 연동 패키지(RMySQL) (0) | 2014.06.04 |
| 샤이니(Shiny) 함수 (0) | 2014.05.04 |




