그래프 개념 및 알고리즘
그래프
수학에서 객체 간에 짝을 이루는 관계를 모델링하기 위해 사용되는 수학 구조인 그래프에 대한 개념

- 그래프는 순서쌍(G=(V, E))으로 볼 수 있으며, 여기에서 집한 V는 점(Vertex, Node), E(Edge, Relationship)는 간선을 의미함
- 그래프는 점 또는 2개의 점을 연결하는 간선으로 구성되어 있고, 간선의 길이나 점의 위치는 중요하지 않으므로 그래프는 조합론적인 대상
- 그래프 이론의 시초는 레온하르트 오일러가 1736년에 쓴 쾨니히스베르크의 다리 문제에 대한 논문으로 여겨짐
- 이 논문에서 오일러는 그래프의 한붓 그리기 존재 여부에 대한 간단한 필요충분조건을 제시함
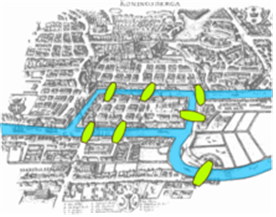
* 쾨니히스베르크의 다리 문제에서 오일러는 각 다리에 A~G까지 부여하여 도식화된 그림에서 해당 문제가 불가능함을 증명하였고 모든 정점이 짝 수개의 차수(Degree)를 갖는다면 모든 다리를 한 번씩만 건너서 도달하는 것이 성립한다고 말하였음. 그로부터 100년이 지나 1873년, 독일의 수학자 칼 히어홀저(Carl Hierholzer)가 이를 수학적으로 증명함. 이를 오일러의 정리(Euler's Theorem)이라 부르며, 모든 간선을 한 번씩 방문하는 유한 그래프(Finite Graph)를 일컬어 오일러 경로(Eulerian Trail/Eulerin Path)라 부른다. 한붓그리기 처럼 글자 그대로 붓을 한 번도 떼지 않고 모든 간선을 한 번씩만 그릴 수 있는지를 의미 한다. 증명에 따르면 쾨니히스베르크의 다리는 모든 정점이 짝수개의 차수를 갖지 않으므로(심지어 짝수개의 차수를 갖는 정점은 하나도 없음) 오일어 경로가 아니다.
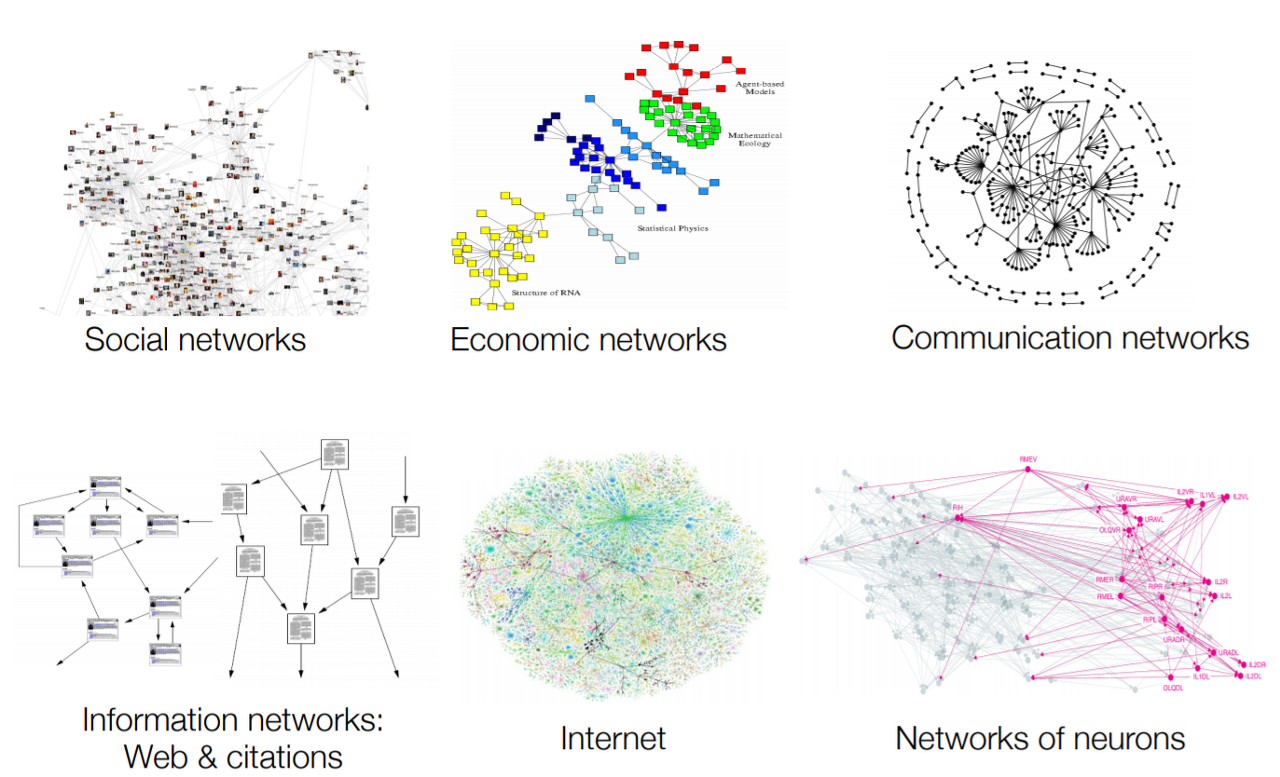
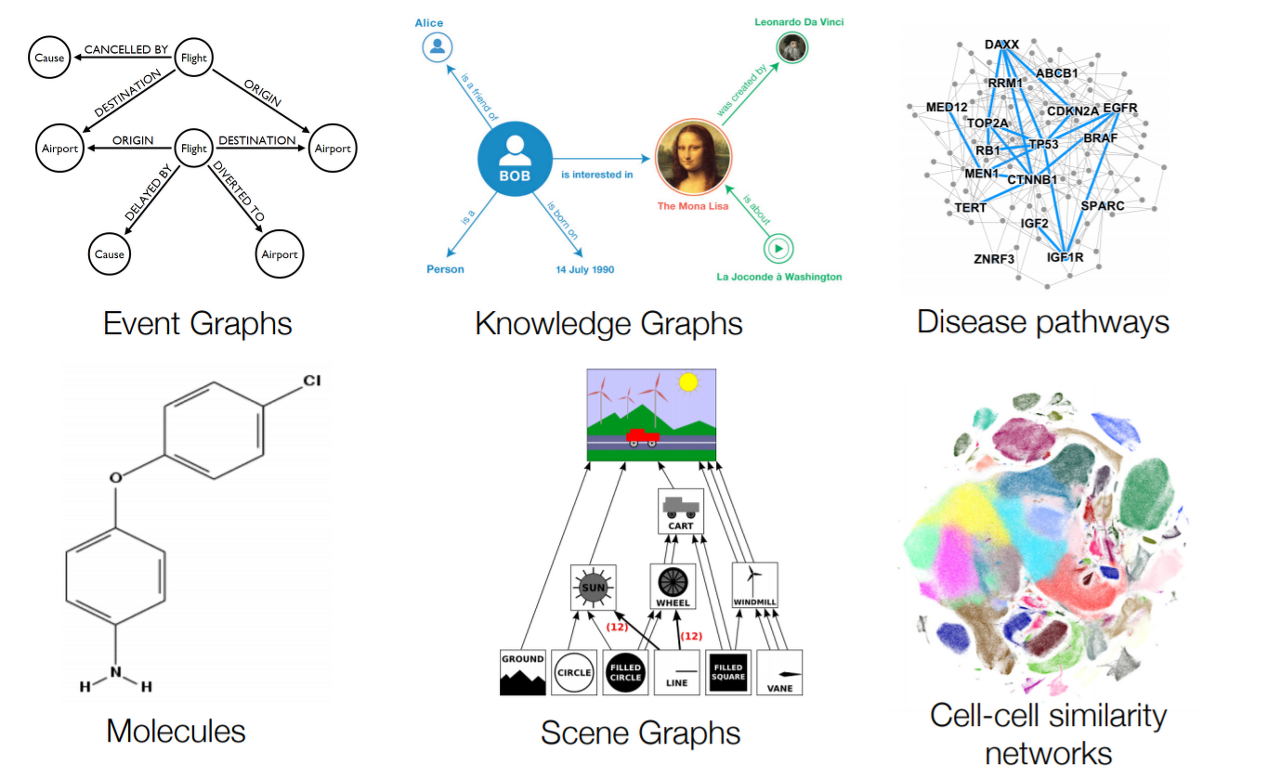
그래프는 지식그래프, 소셜 네트워크, 추천 시스템 등 다양한 분야에서 사용 될 수 있다.
방향 그래프 / 무방향 그래프
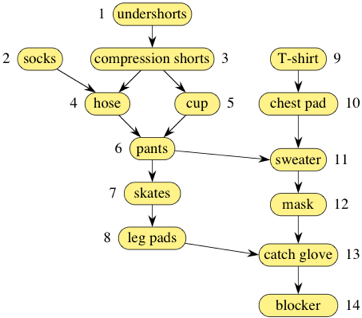
- 점 사이의 연결이 항상 양방향인 것은 아니며 도로를 예로 들면 일방통행 길이 있을 수 있음
- 위는 아이스하키에서 골키퍼가 옷을 입는 순서를 나타낸 그래프
- 화살표로 나타나는 연결은 방향성이 있으므로(directed) 이 그래프는 방향 그래프(directed graph)임
- 방향은 어떤 장비를 다른 장비보다 먼저 입어야 하는지는 나타내고 있으며 가슴 패드에서 스웨터로 가는 방향은 스웨터를 입기전에 가슴 패드를 착용해야 한다는 것을 가리킴
- 이러한 그래프를 방향성 비순환 그래프(directed acyclic graph, dag)라고 함
가중치 그래프
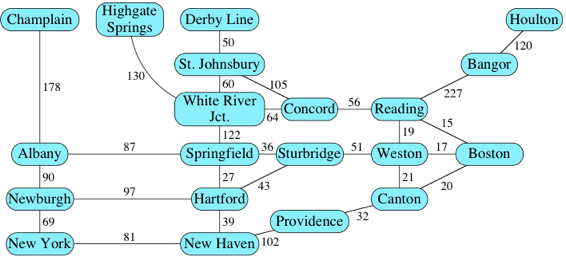
- 위의 그래프에서 연결관계마다 특정 값을 부여한 가중치를 나타낼 수 있음
- 이러한 그래프를 가중 그래프(weighted graph)라고 함
- 도로 지도의 경우 두 곳 간의 최단 경로를 알고 싶으면 두 정점 간의 모든 경로에서 변의 가중치 합이 최소가 되는 경로를 찾으며 이런 경로를 최단 경로(shortest path)라고 함
- 위의 그래프에서 뉴욕(New York)에서 콩코드(Concord)로 가는 최단 거리는 뉴욕-뉴헤븐-하트퍼드-스터브릿지-웨스턴-리딩-콩코드로 이어지는 총 289마일의 경로임
그래프 알고리즘
위의 방향성 그래프와 가중치 그래프를 탐색하면서 원하는 정보를 찾을 수 있지만 대규모의 그래프에서는 원하는 정보를 찾기란 사막에서 바늘 찾기와 같은 수준이다. 그래프 알고리즘을 이용하면 대규모 그래프에서 어떤 정점이 영향력 높은 정점인지 또는 각각의 정점은 어떤 그룹이 형성되는지를 파악할 수 있으며 원하는 정점을 찾기 위한 최단 거리를 탐색하는 등의 분석을 수행 할 수 있으며 그래프 알고리즘은 대표적으로 아래와 같음
경로 찾기
경로 찾기 알고리즘은 그래프 분석의 기본으로 그래프 탐색 알고리즘을 기반으로 노드 간 경로를 탐색하고 하나의 노드에서 시작해 목적 노드에 도달할 때까지 관계를 탐색함
- 경로찾기 알고리즘 종류
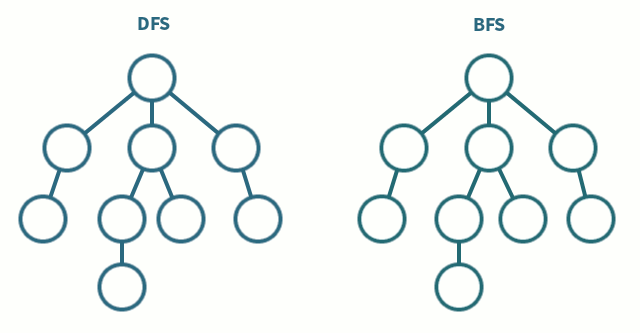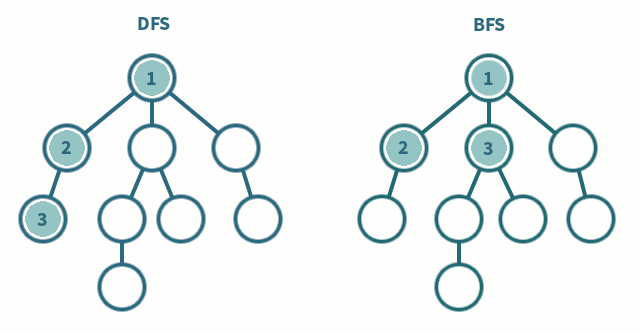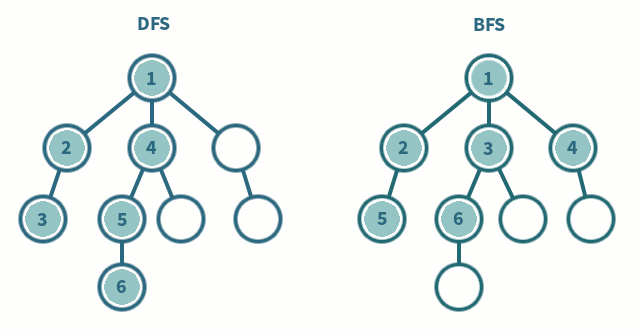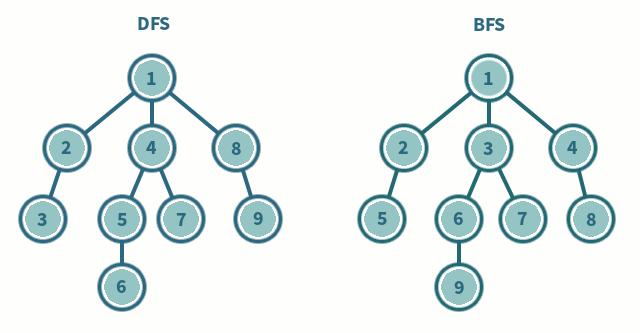
* BFS(Breadth First Search) : 기본 그래프 순회 알고리즘 중 하나이며, 선택한 노드에서 시작해 두 홉 떨어진 모든 이웃을 방문하기 전에 한 홉 떨어진 모든 이웃을 탐색하는 알고리즘
* DFS(Depth First Search) : 또 다른 기본 그래프 순회 알고리즘이며, 선택 노드에서 시작해 인접 노드 중 하나를 선택한 다음 역추적하기 전에 해당 경로를 따라 가능한 깊이 탐색하는 알고리즘
* Dijkstra 알고리즘 : 출발 노드에서 기작하여 가까운 노드부터 시작하여 모든 방향으로 확장해가며 그래프에 있는 노드들을 방문하여 목표 노드까지의 경로를 검색. Dijkstra 알고리즘은 비효율적이지만 출발 노드에서 목표 노드까지 항상 최단의 경로를 찾을 수 있는 장점이 있음
* Best-First Search : Dijkstra 알고리즘과 비슷하게 동작하지만 임의의 노드에서 목표 노드까지 거리가 얼마나 되는지 휴리스틱 추정치를 사용하며, 출발 노드에서 가장 가까운 노드를 선택하는 대신에 목표 노드에 가장 가까운 노드를 선택. Best-First-Search 알고리즘은 목표 노드에 이르는 경로를 안내하는 휴리스틱 함수를 사용하기 때문에 Dijkstra 알고리즘보다 훨씬 빠르게 수행하지만, 최단 경로를 보장하지 못함.
* A*알고리즘 : Dijkstra 알고리즘과 Best-First-Search 알고리즘의 장점을 이용하여 고안되었으며, 일반적인 휴리스틱 방법은 최선의 해를 제공하지 못하고 근사적인 해를 제공하지만 A* 알고리즘은 휴리스틱 방법으로 설계되었음에도 최단 경로를 보장함
* Yen's 알고리즘 : 최단 경로 알고리즘과 유사하자미나 두 쌍의 노드 사이에서 최단 경로만 찾는 것이 아니라 두 번째 최단 경로, 세 번째 최단 경로 등 최단 경로의 -1 편차 등을 최대 k까지 계산. 최단 경로를 찾는 것이 최대 목표가 아닐 때 대체 경로를 얻을 수 있다는 장점이 있음
중심성
그래프 내에서 어떤 노드가 영향력이 있는지를 파악하기 위한 알고리즘이며 그래프(네트워크) 내에서 노드가 차지하는 중심적 위지, 노드가 가지는 파워, 영향력, 네트워크 내에서 어떤 노드가 더 중요한지를 식별하고 신뢰성, 접근성, 사물이 퍼지는 속도, 그룹 간 브리지와 같은 집단 역학을 이해하는데 도움이 됨
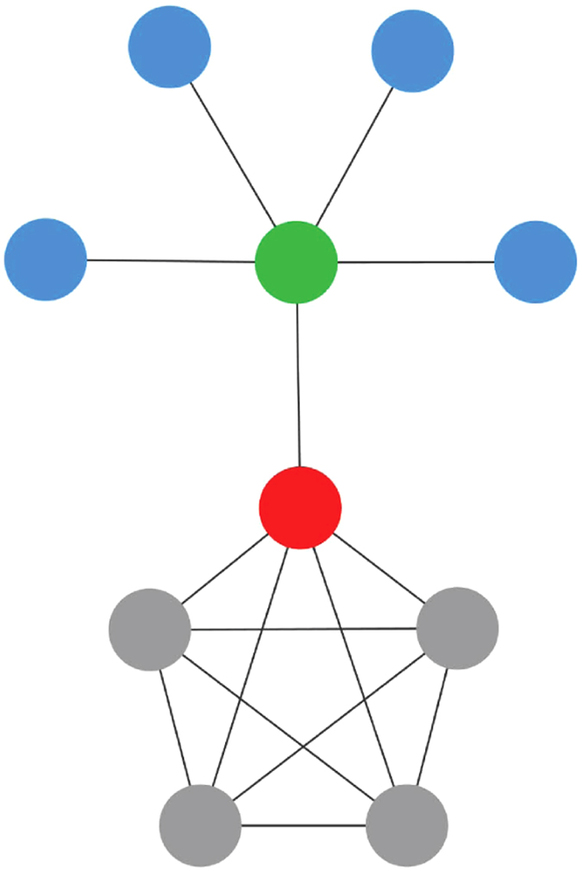
- 중심성 알고리즘 종류
* 연결 중심성(Degree Centrality) : 가장 간단한 중심성 척도이며, 방향성이 있는 그래프는 In-Degree만 계산할 경우 그 노드의 인기도를 볼 수 있으며 Out-Degree만 계산할 경우 그 노드의 영향력을 볼 수 있음
* 페이지 랭크(Page Rank) : 지금의 구글을 있게 만든 알고리즘이며 웹 페이지에 대한 중요성을 판단하는 방법을 그래프에 적용하게 되면 노드에 들어오는 관계의 수와 중요성을 측정하여 계산하고 단순히 많이 링크된 노드를 중요 노드로 판단하기 보다는 중요한 노드로부터 링크를 받는 노드의 중요성도 높게 측정되어짐

* 고유벡터 중심성(Eigenvector Centrality) : 페이지 랭크 알고리즘과 비슷하게 연결된 노드가 많다고 해서 반드시 중요한 노드가 아니므로 연결된 노드의 중요성에 따라 차별적으로 반영하여 중요성을 판단
* 매개 중심성(Betweenness Centrality) : 두 노드 사이에 특정 노드를 거쳐가는 경우가 많을 수록 특정 노드가 중요하다고 판단하는 알고리즘. 즉, 해당 노드가 매개체 역할을 얼마나 잘하는지를 측정함. 매개중심성이 크다면 네트워크 내의 의사소통 흐름에 영향을 줄 수 있거나 해당 노드가 없을 경우 전체 네트워크 흐름에 영향을 받게 됨
* 근접 중심성(Closeness Centrality) : 중요한 노드일 수록 다른 노드까지 도달하는 경로가 짧을 것이라는 가정을 기저에 두고 있으며, 한 노드 i에서 i를 제외한 다른 노드들까지의 최단 경로의 길이를 평균을 내고 그 값을 역수로 취하여 계산함
* 그 외에 Article Rank, Eccentricity Centrality, 조화 중심성(Harmony Centrality), 카츠 중심성(Katz Centrality) 등 다양한 중심성 알고리즘이 존재함
커뮤티니 탐지
그래프 내에서 동일한 커뮤니티(유사 그룹)가 형성되는 커뮤니티를 찾는 알고리즘으로 노드 클러스터, 격리된 그룹, 전체 네트워크 구조 등을 파악할 수 있음
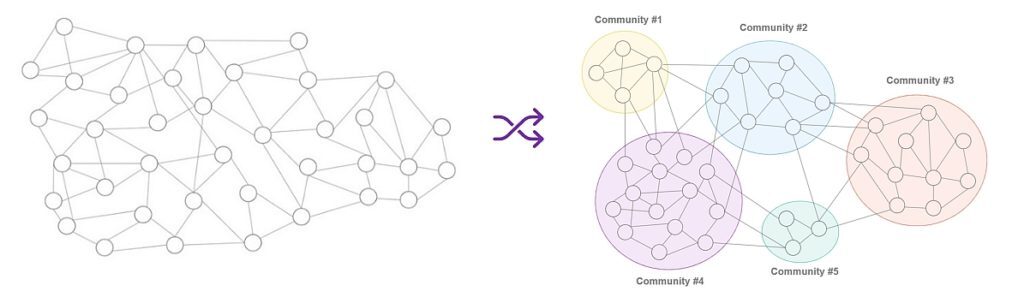
- 커뮤니티 탐지 알고리즘 종류
* 전체 관계 밀도에 대한 트라이앵글 수와 결집 계수
* 연결 클러스터를 찾기 위한 강한 요소와 연결
* 노드 레이블을 기반으로 그룹의 신속 추론을 위한 레이블 전파
* 그룹화 품질과 계층 구조를 살펴보는 루뱅 모듈성
그래프 임베딩
그래프 데이터(정점)을 벡터의 형태로 표현하는 방법
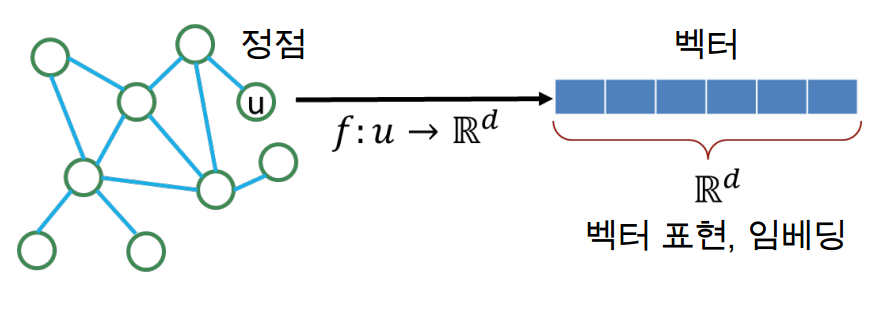
그래프에서의 정점간 유사도를 임베딩 공간에서도 “보존”하는 것을 목표함
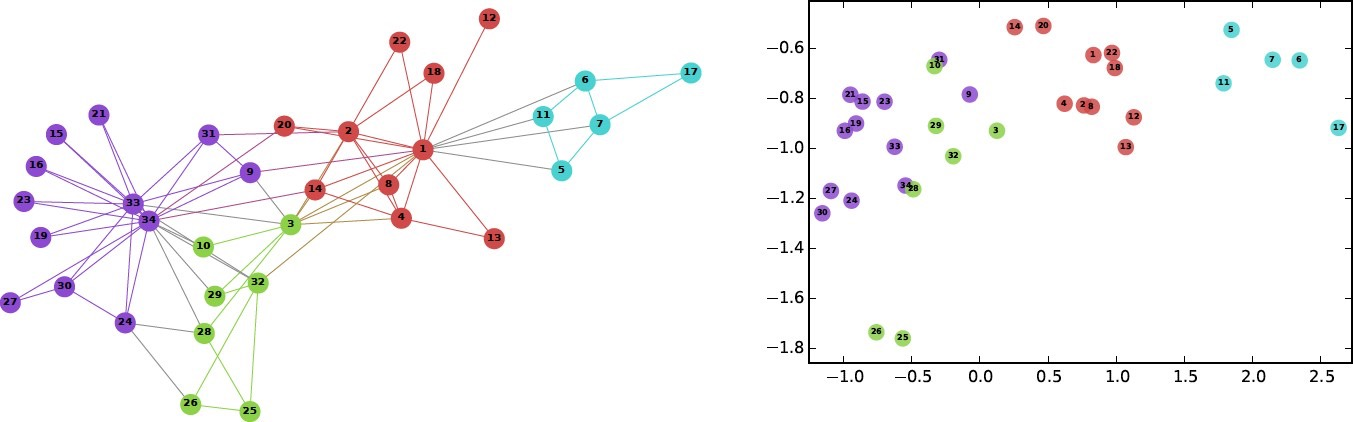
- 그래프 임베딩 알고리즘 종류
* GNN(그래프 뉴럴 네트워크)
* GCN(그래프 컨볼류션 뉴럴네트워크)
* GAT(그래프 어텐션 네트워크)
* GraphSAGE
* 위의 종류 뿐만 아니라 다양한 그래프 임베딩 알고리즘이 연구되고 있음
ㅁ 참고자료
http://contents2.kocw.or.kr/KOCW/document/2015/pukyong/kwonoeum/6.pdf
https://www.boostcourse.org/ai211
그래프와 추천 시스템
부스트코스 무료 강의
www.boostcourse.org
https://ko.wikipedia.org/wiki/%EA%B7%B8%EB%9E%98%ED%94%84_%EC%9D%B4%EB%A1%A0
그래프 이론 - 위키백과, 우리 모두의 백과사전
ko.wikipedia.org
그래프 설명하기 (개념 이해하기) | 알고리즘 | Khan Academy
ko.khanacademy.org
쾨니히스베르크 다리 건너기 문제 - 나무위키
이 저작물은 CC BY-NC-SA 2.0 KR에 따라 이용할 수 있습니다. (단, 라이선스가 명시된 일부 문서 및 삽화 제외) 기여하신 문서의 저작권은 각 기여자에게 있으며, 각 기여자는 기여하신 부분의 저작권
namu.wiki
쾨니히스베르크의 다리 문제 - 위키백과, 우리 모두의 백과사전
ko.wikipedia.org
https://bab2min.tistory.com/554
[네트워크 이론] 다양한 중심성(Centrality) 척도들
세상의 많은 관계들을 수학적으로 나타내는데에는 그래프만큼 강력한 도구도 없습니다. 관계의 주체가 되는 행위자들은 Node로, 관계들은 Node사이를 연결하는 Edge로 나타낼 수 있기 때문이죠. 이
bab2min.tistory.com
책 - 그래프 알고리즘